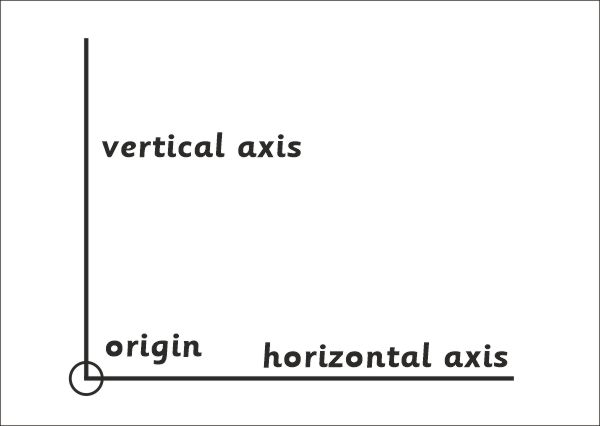
Diagram showing two axes and the origin ~ the origin is a small dot ~
too small to show ~ so I have drawn a circle around it
You will need a sheet of A4 graph paper with millimetre divisions. You will only be using half of it. Paper with larger squares would be better, but it is unlikely that an A4 sheet would be large enough. Alternatively a sheet of plain paper with a ruler and set square will do the job. A sharp pencil, and some neat and accurate working is required.
You need to know what a square is ~ and some of its properties ~ and it will help if you know a good way of drawing them easily ~ a small set square helps. You will need to follow simple instructions ~ quite a few of them. I think it will be worth it.You will need to do some simple adding and subtracting. Finally ~ the hardest bit ~ you will need to do some straightforward ~ logical ~ thinking.
Near the bottom left hand corner of your sheet mark a small dot or point. For work like this I would call it the origin. From the origin draw a horizontal line across your page. It will need to be about 12cm long ~ or 120mm. Then draw a line at right angles ~ perpendicular ~ to this ~ also through the origin. Again ~about 12cm. It will be called the vertical axis. In maths and science these two lines are called axes.

From now on you will be asked to draw ~ accurately ~ squares. From time to time I will show you what my version looks like.
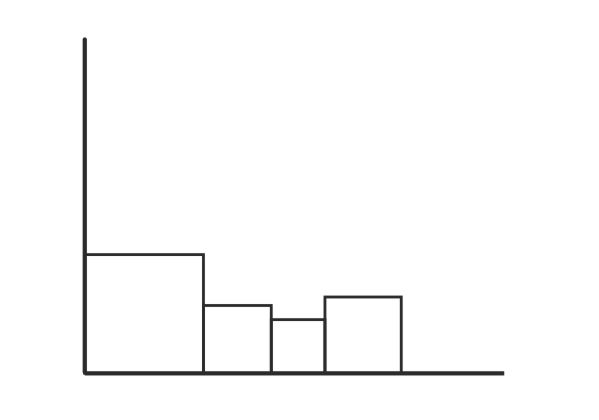
With the origin at one corner ~ draw a square with sides of 42mm ~ with its base on the horizontal axis and one side on the vertical axis.
When you have done this draw second square ~ of side 24mm ~ adjacent to the first ~ further away from the origin ~ still on the axis.
Adjacent to that ~ moving along horizontally ~ a third square of side 19mm.
Finally draw another ~ still on axis ~ still horizontally adjacent to the previous square ~ of side 27mm.
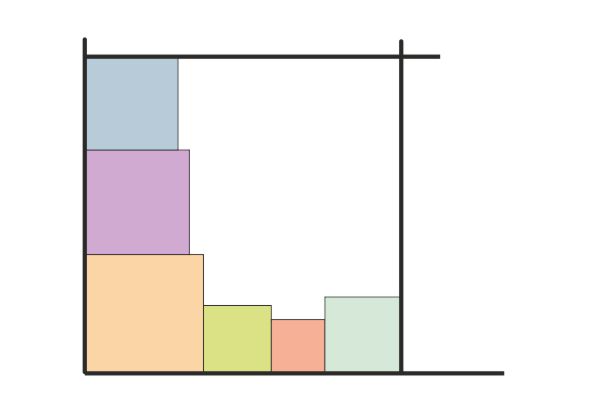
Here is a sketch of what you should have at this stage ~
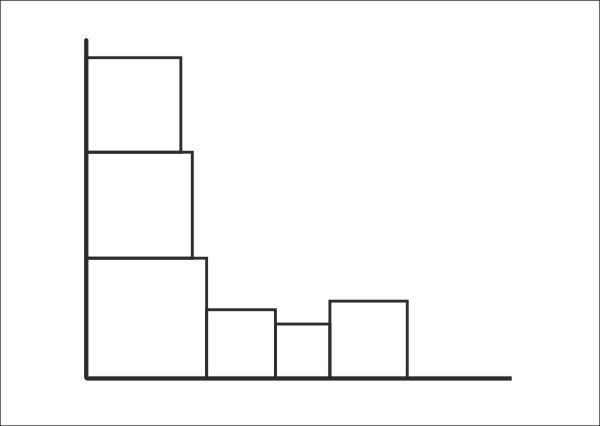
Go back to the first square ~ the one drawn by the origin ~ and draw another square with sides of 37mm ~ vertically above the first square ~ touching the vertical axis.
Again ~ vertically adjacent to the previous square ~ above it ~ left side on the axis ~ draw a square of side 33mm. You should by now have a rather raggedy looking 'L' shape made of six squares.
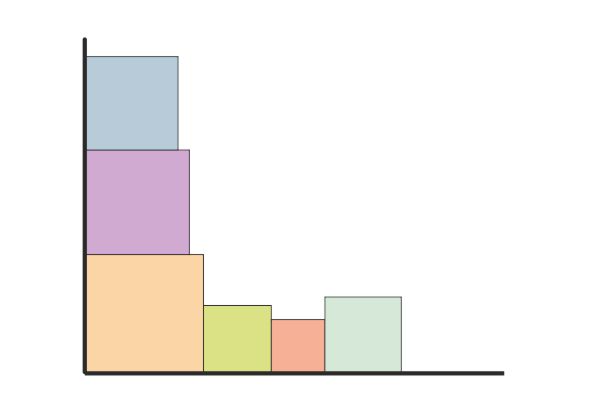
If you wish ~ you could colour the squares at any time you like.
Next draw a horizontal line across the page such that the top side of the last square you have drawn ~ the 33mm sided square ~ is extended out to the right by a fair way. Then draw a vertical line perpendicular to the horizontal axis and starting along one side of the 27mm square. These two lines will meet in such a way that you now have a huge square with some smaller squares inside it.
A hundred years ago a Russian mathematician suggested that it was not possible to fill ~ completely ~ with no gaps ~ all the remaining space inside the large containing square ~ with lots of smaller squares ~ every square to be a different size.
Some years later a German mathematician showed him to be wrong. He filled a different ~ larger ~ containing square with 55 ~ all different ~ smaller ~ squares.
Some years after that a Dutch mathematician discovered several solutions to the Fill a Square with Squares problem. Each solution contained 22 squares. He used a computer to help him with lots of different squares.He eventually found the best solution yet ~ where 'best' is the smallest number of squares ~ all different ~ to fit inside a big one.
I have helped you a lot. You can do the rest of the task ~ and tick off all four successes listed above.
Your task ~ now ~ is to complete this jig saw ~ with more squares of any size not already used. There is no need for trial and error ~ you can work it out bit by bit ~ provided your next step is to draw a 50mm square in the corner that is so far unoccupied.
I will give you two more clues ~ and pictures ~ to set you on the right track ~
You have to fill the raggedy white 'L' shape ~ below ~ with squares ~ of any size ~ no two squares the same. There is just one square that fits in the space at the top of the containing square ~ and just one other square to fit in on the right hand side of the container.
After that you can find the rest of what was once declared an impossible solution. You will also be able to answer my quesion ~
You do need to draw things neatly ~ one of the squares could easily get lost ~ it is a tiny 2mmx2mm.
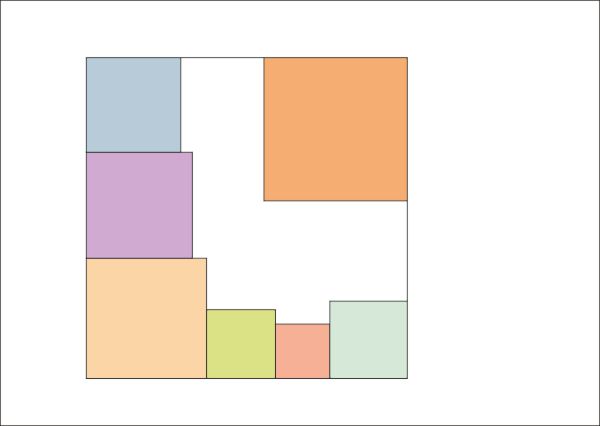
There are several related tasks that you could tackle ~
~ You have provided a convincing demonstration. There is another well known convincing demonstration that is actually wrong. Try it. After than you might be able to devise a mathematical proof that your demonstration is correct ~ and that it has not missed a 1mm square somewhere!
~ There are some easier tasks involving filling rectangles with squares. I may find time to write about them ~ or you might be able to look them up somewhere.
~ Do not be tempted to find any other solutions by trial and error ~ there are many more important things to do in life. It has been proved (somehow) that there are no answers of 20 or less ~ so that would be futile. No doubt many other solutions have been found and recorded ~ I have not checked. However ~ read on
~ I suspect that a good programmer could write a program to 'discover' what the Dutchman did ~ and solve the problem. I cannot program computers, and so can offer no guidance on this. I do know that computers ~ and human skills ~ have improved immensely since the days of the earlier discoveries.
