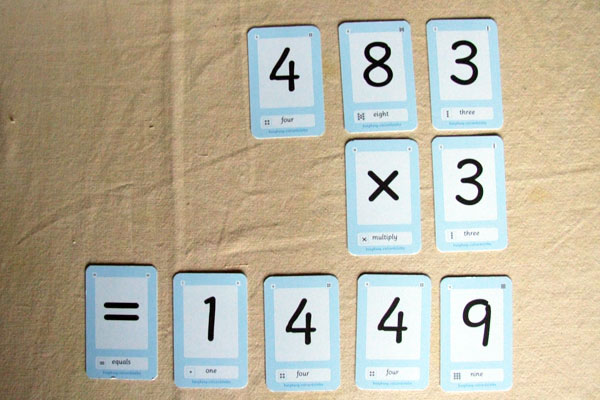
Here is the multiplication part ~ 3 × a
The first person to make a note of all this was a philosopher called Iamblichus. He did not set the problem out as I have done. We know he did it, since some of his writings, and those of his pupils, have survived. He found something out which I find interesting. Maybe you will...
Think of a number and call it a. (Note: There are some pictures, below, that may help you check your progress. They leave out some of the work you have to do. I have chosen ~ for no particular reason ~ the number 483 in the picture below.)
Work out 3 × a + 1...Write it down...Call it b

(Note:If an expression contains + signs and × signs you must work out the multiplication first of all. In this case if you work from left to right that will be fine. Mathematicians are very keen on making things as short as possible. They have a convention that 3 × a can be written as 3.a or ~ better ~ 3a).
Work out 3 × a + 2...Write it down...Call it c

Work out 3 × a + 3...Write it down...Call it d
Add up the numbers b + c + d...Call the result e

Label the digits of your result eas f, g, h, j,... (Notes: You can do this in your mind ~ no need to write anything down. The labels are to help you understand the next instruction. You may have two or three such digits, or possibly four. It is good practice for a mathematician not to use i that is why I have missed it out.)
Add up your digits f + g + h + j ... If the result still has more than one digit...add them again...Keep repeating until you end up with just a single digit.


You should end up with just one digit.Atthatpoint cannot add that to anything. If you do not ~ eventually ~ end up with a single digit ~ take a moment to review what you have done ~ checking there were no mistakes.
Repeat everything again with a different starting number. The larger the better! (You could use a calculator for very large numbers.)
Stop when you have reached a discovery that you can be fairly sure may be interesting and true. I am sure you will know when you have reached that point. Maybe it will take three or four repeats. Maybe ~ if you do it many times ~ you will find an exception ~ maybe not.
